When it comes to building high-performance numerical applications you often find people sacrificing maintainability and abstraction for the sake of performance. While I typically argue that these optimizations are premature, I wanted to investigate this issue a little bit more in detail.

I went ahead and did a little experiment in Rust. Rust is a new programming language developed by Mozilla and a currently very active and open community of contributors. I like it quite a lot due to its goal to be a safe, performant and concurrent language with a modern object model that helps you create and maintain abstraction boundaries between different layers of an application.

The (somewhat contrived) problem that I chose to solve is a classical map-reduce scheme. You have some input values (which I simply chose to be a running integer) and want to apply a function to it. The end result is the sum of all the function values obtained in this way.

The most primitive algorithm is completely imperative and manages all variables in the same scope:

// loop.rs
use std::os;

fn main() {
    // Parse parameters
    let args = os::args();
    assert!(args.len() == 3, "must have two arguments");
    let total: int = from_str(args[1]).unwrap();
    let k: int = from_str(args[2]).unwrap();
    let n: int = total / k;

    // Summing up
    let mut s: f64 = 0.0;
    let mut si: f64;
    let mut i: int = 0;
    let mut j: int;
    while i < n {
        // Computational kernel
        j = 0;
        si = 0.0;
        while j < k {
            si += ((j + i) as f64) * 13.41 + 9.71;
            j += 1;
        }
        s += si;
        i += 1;
    }
    println!("{:f}", s);
}

Now this is obviously not so pretty, since the computational kernel is hard-coded into the main function. We can improve on that:

// loop_fct.rs
use std::os;

/// Computational kernel
fn kernel(i: int, k: int, a: f64, b: f64) -> f64 {
    let mut si = 0.0;
    let mut j = 0;
    while j < k {
        si += ((j + i) as f64) * a + b;
        j += 1;
    }
    si
}


fn main() {
    // Parse parameters
    let args = os::args();
    assert!(args.len() == 3, "must have two arguments");
    let total: int = from_str(args[1]).unwrap();
    let k: int = from_str(args[2]).unwrap();
    let n: int = total / k;

    // Summing up
    let mut s: f64 = 0.0;
    let mut i: int = 0;
    while i < n {
        s += kernel(i, k, 13.41, 9.71);
        i += 1;
    }

    // Output
    println!("{:f}", s);
}

This is already a bit nicer. However, we might require some more run-time flexibility and would like to talk about the computational kernel not as a static function but rather as an abstract interface, which may have several implementations. It might be useful to be able to dynamically dispatch to one of these depending on certain run-time criteria.

Rust has traits and structs to implement this safely. I did not actually implement different kernels, since this would be hard to compare to the static case that does not have this run-time flexibility. So in the following code there is only one implementation, which still must be dynamically dispatched to allow for a comparison of performance.

// rust_trait.rs
use std::os;

/// Abstract computational kernel
trait ComputationalKernel {
    fn calc(&self, i: int) -> f64;
}

/// Kernel implementation that sums up some linear terms
struct SumLinearTermsKernel {
    a: f64,
    b: f64,
    k: int,
}

impl ComputationalKernel for SumLinearTermsKernel {
    fn calc(&self, i: int) -> f64 {
        let mut si = 0.0;
        let mut j = 0;
        while j < self.k {
            si += ((j + i) as f64) * self.a + self.b;
            j += 1;
        }
        si
    }
}

/// Main function
fn main() {
    // Parse parameters
    let args = os::args();
    assert!(args.len() == 3, "must have two arguments");
    let total: int = from_str(args[1]).unwrap();
    let k: int = from_str(args[2]).unwrap();
    let n: int = total / k;

    // Summing up
    let mut s: f64 = 0.0;
    let mut i: int = 0;
    let kernel: ~ComputationalKernel = ~SumLinearTermsKernel{a: 13.41, b: 9.71, k: k};
    while i < n {
        s += kernel.calc(i);
        i += 1;
    }

    // Output
    println!("{:f}", s);
}

This is more complex considering the specific task at hand but it would be much more flexible to use in a different context or to combine with other implementations.

So, let's see how long it takes to execute the programs. Each program accepts two input parameters declared as total and k in the main function. If you analyse the algorithms, you'll see that total is an effective measure for the total numerical cost, while k controls the cost of a single call to the computational kernel.

I made test runs for total = 2·10⁹ and k running from 1 to 100. The results in terms of execution time can be seen in this diagram:

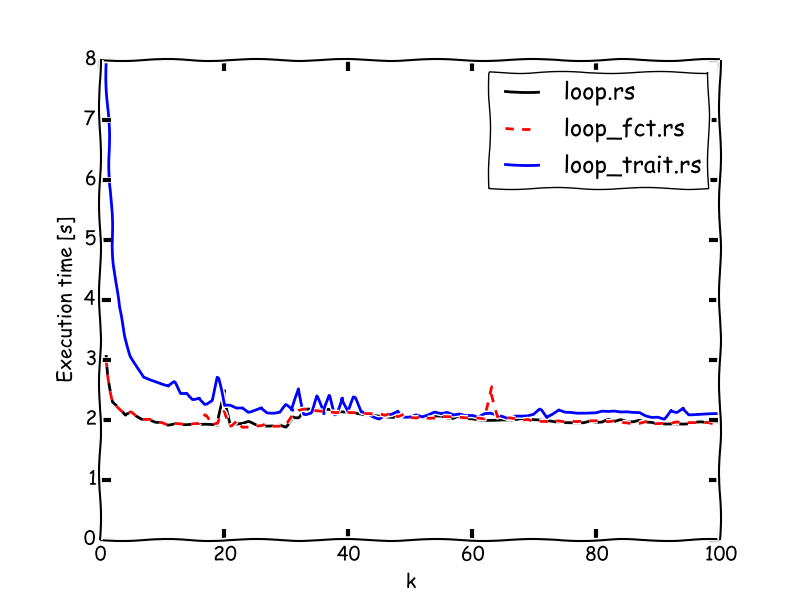
(Note: I chose matplotlib's xkcd-style plot, because this is not exactly a rigorous scientific study despite the exact values.)

The result is pretty much as expected, though the quantitative assessment is something that one should keep in mind when thinking about whether the polymorphic overhead is to be considered harmful.

In summary:

• There is virtually no difference between the spaghetti code and the version wrapped into a function. Inlining appears to be efficient enough to always allow for static functions.
• Polymorphism comes at a price of about a factor two for small functions. The difference is negligible for functions worth more than 30 simple (linear) formulae.
• There is some odd performance loss for the non-polymorphic versions at about k = 30. I have no idea what the reason for this is, maybe someone with more knowledge about compiler optimizations, specifically in rustc and LLVM can shed light on this.

As a conclusion I would say that the performance hit here is not bad enough to worry about it in Rust. You certainly could try to avoid the use of dynamic type resolution for primitive operations, when the flexibility is not required. But when it is necessary, I would not hesitate to use a polymorphic object model to address these issues.

One has to keep in mind that avoiding polymorphic method calls leads necessarily to some other kind of dispatch mechanism, which may very well be less generic, type-safe, maintainable or performant than the dynamic vtable dispatch used for traits.

However, please view these numbers with caution. They may or may not apply to a in fundamentally different use case and are obviously subject to optimizations and implementation details of the Rust compiler and LLVM.

For reference, you can find the source code here. I tagged the revision used for this blog post as blog-20140228.

Note: there is a follow-up article to this one by now, which expands on this one.